7.3.4 Periodic O-Lattices and Pattern Elements

A CSL lattice by definition has coincidence points in both lattices; the CSL points thus are always O-lattice points, too. The converse is not necessarily true (as we already have seen in the example):

The O-lattice of two crystals in a CSL orientation thus must include the CSL lattice points as O-lattice points. This O-lattice, however, may also have additional O-lattice points - all we can deduce at this point is that the CSL lattice points must be a subset of the O-lattice points which belong to the O-lattice that includes the specific CSL orientation.

We know that the CSL points are O-points which are always of the same equivalence type - they are lattice points, to be precise. In other words, the O-lattice belonging to a certain CSL lattice, if drawn into the coordinate system of one of the crystals is periodic in this reference system.

This is not a general property of an O-lattice - in general, every equivalence point defined by an O-point could be different from all the others and there would be no periodicity.

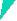This is best visualized by drawing all equivalence points encountered for a given O-lattice (which, of course, always has infinitely many points) into the unit cell of one of the crystals - we obtain the so-called reduced O-lattice.

For a periodic reduced O-lattice, there would be a finite number of equivalence points; a non-periodic lattice would lead to an infinite number of equivalence points in the reduced O-lattice.

Lets look at some examples:

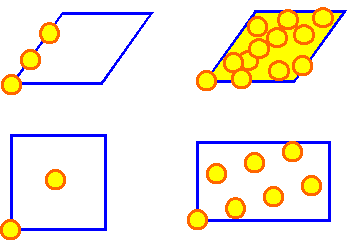
Shown are elementary cells of one lattice (blue) with the equivalence points occurring in the O-lattice drawn in. In three cases the O-lattice would be periodic; in the case in the upper right, it would be non-periodic

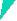Periodic O-lattices are clearly special; and it is self-evident that every CSL orientation must correspond to a periodic O-lattice. But there is more.

At any O-lattice point in a periodic O-lattice, we have a certain arrangement of the crystal atoms around that point, a specific pattern. Since in a periodic O-lattice there are only a finite number of different equivalence points, there is only a finite number of distinct patterns, too.

An individual pattern is called a pattern element. There are as many pattern elements as there are equivalent points in the reduced O-lattice.

This is a crucial concept in O-lattice theory, unfortunately it is not explained very well in Bollmanns book. Let's see what is meant by pattern:

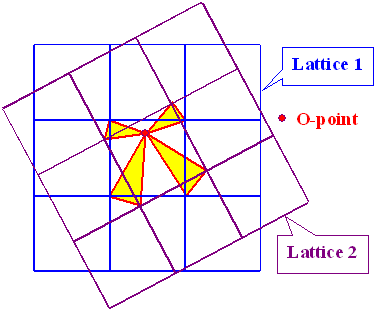
Shown are two lattices (blue and magenta which are superimposed) and one O-point (red). A representation of the geometry of the atoms that you may put into the lattices is given by the yellow triangles. They are simply constructed by connecting the lattice points of the two lattices "around" the O-point with the O-point.

The picture also demonstrates (but does not prove) an universal theorem: Any O-point can be chosen as the origin for the transformation that produces lattice 2 from lattice 1 (here it is a simple rotation).

In a non-periodic O-lattice, the representation of patterns in the way shown is different at any O-point - this is also rather difficult to draw.

This is where O-lattice theory gets hard to illustrate. Nobody surpasses Bollmann who provides complicated drawings of patterns (done by hand!) in his book, one example is shown in the link.

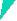The question now is: Which orientations provide periodic O-lattices? It appears that there is no simple formula coming up with transformation matrices or angles for rotations that produce periodic O-lattices. We have to go the other way and ask two questions for any possible orientation:

Is the corresponding O-lattice periodic?

If yes, how many pattern elements (= N) are contained in the reduced O-lattice?

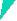What we want is N as a function of some misorientation angle for some simple geometries. This needs some numerical calculations; lets look at the results for rotations on the {110} planes of cubic crystals

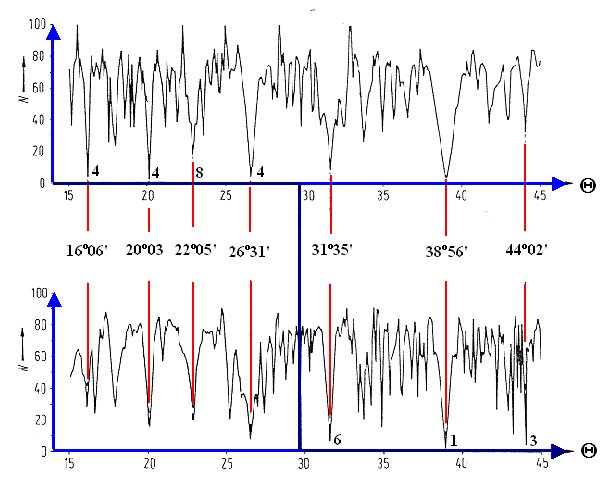
The following picture shows N as a function of the misorientation angle:

This again is one of Bollmanns trickier pictures (with some color added), because it is only understandable if you read and understood much of what has been said before in his book (it is neither explained what the difference is between the two curves - they have after all an identical coordinate system, nor what the bold lines (here dark blue) implicate).

Well, the N-values are given for two independent kinds of transformations which both include the same rotation T (upper and lower curve), but one inlcudes a so-called "unimodular transformation" in addition. The one with the smallest determinant which, as we have seen, is the one you should use, changes from the upper curve to the lower curve at T = 30^o and this explains the bold (or dark blue) lines. Since the two curves are different, you now see that it matters, indeed, which transformation matrix you pick.

Don't worry; it is not necessary to understand that in detail. Just acknowledge, that N can be computed and that unambiguities with respect to different transformation matrices can be dealt with somehow.

Also note that the "real" curve would be a fractal with N = ∞ for most values; it is smoothed here by only counting the equivalence points in 100 "pixels" of the O-lattice (so N ³ 100 applies) and stopping the numerical procedure after some time if it does not turn periodic anyway.

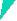It is clear that there are several "special" orientations for this geometry with small values of N. This looks good, however, we are not yet done. We are really looking for O-lattices that are periodic on a short scale, i.e. the patterns should repeat after a short distance. This requires three ingredients:

Periodicity as a starter, i.e. N is finite (or in reality e.g. N < 100 for numerical calculation).

Small values of N, because the pattern repeats after N steps - the larger N, the longer it takes for a repetition. To give an example: For N = 10 you have to go out 10 lattice constants of the O-lattice before the same pattern is encountered again.

This immediately calls for small lattice constants of the O-lattice, too. Or, to be more general, for small volumes V_O of the O-lattice cells.

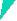The real measure for the periodicity of the O-lattice patterns is therefore not N, but the density N' of periodic equivalence points given by

N'	=	N V_O	=	N \|T\|

With |T| meaning the determinant of the transformation matrix, since V_O = 1/ |T| follows from basic matrix algebra together with the definition of the O-lattice.

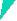Now comes a major point: N' is nothing but the number of crystal units (volume of unit cells or lattice constants) per period of the pattern because the unit of the O-lattice is always (for periodic O-lattices) an integer number of the crystal units!

In other words: N' corresponds directly to the measure of coincidence in the CSL model, the number Σ! In fact, the numerical values are identical in most (but not all) cases: N' = Σ.

The O-lattice theory, however, is not only much more general, but gives the recipes for calculating N' (or Σ). Try, for example, to find the CSL lattices for orientations between, say a cubic and a monoclinic lattice: All you need are the deformation matrices; the rest can be done for all possible cases by a computer program.

Just one case in point: What happens for perfectly well defined transformation matrices T, but with |T| = 0? N' in this case will be ∞.

Lets look at an example: Rotation of cubic lattices by an angle around a <110> direction:

Angle Θ	\|T\|	N	N´	Σ
10^o 6,0´	0,031	4	129	129
13^o 26,06	0,055	4	73	73
20^o 3,0´	0,121	4	33	33
22^o 50,4´	0,157	8	51	51
26^o 31,6´	0,210	4	19	19
38^o 56,6´	0,111	1	9	9
50^o 28,6´	0,000		oo	11
58^o 59,6´	-0,030	1	33	33
70^o 31,6´	0,000		oo	3

Two perfectly well defined rotations lead to |T| = 0; their Σ values are 11 and 3, respectively, while N' is infinity!

This tells us that these particular orientations are much more special then implied by their Σ values: These orientations can be obtained by simpler transformations matrices of lower rank and they correspond to grain boundaries with a particular high degree of "fitting" and thus low energy.

There is also a first real result: Σ11 boundaries should be rather common, and that's what they really are.

We will not go into more details at this point; but it should become clear that there is a lot of power behind the O-lattice theory.

However, even at this stage, calculations become tedious and need numerical methods. It would be most useful to implement the basic equations in a computer program from now on - but I do not know if this has been done.

And, always keep track of this: So far we have only dealt with "small deformation" boundaries and with high angle boundaries having a periodic O-lattice. We are still some distance away from a general boundary.

We now need to do the next step - always, for easier understanding, in analogy to the CSL model of grain boundary structures:

What happens if the orientation of the two crystals (including arbitrary lattices and thus phase boundaries, too) is close to, but not exactly at a "special" O-lattice orientation? "Special" meaning a periodic O-lattice.

In other words, we are asking for possible structural defects which can be superimposed and will change the (generally non-periodic) O-lattice of an arbitrary boundary (which is always defined) just the right amount to generate a periodic O-lattice with a supposedly low energy?

This is the essentially the same question we asked for crystals close to, but not exactly at a " low Σ" orientation - but on a much higher level of abstraction and with the possibility to deal with it quantitatively.