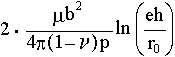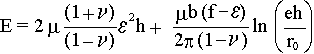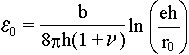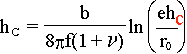Nucleation and Propagation of Misfit Dislocations in Strained Epitaxial Layer Systems

P.B. Hirsch

(Sir Peter)

Department of Materials, University of Oxford

The annotated version

Comments on light blue background

1. Introduction

In 1949 Frank and van der Merwe [1] discussed theoretically the stresses and the energies at the interface of an epitaxial layer grown on a matrix with a slightly different lattice parameter. Their one-dimensional model was extended to two dimensions by Jesser et al.[2]. These studies show that if the lattice mismatch is small, and/or the thickness of the overlayer is not large, the growth of the epilayer is pseudomorphic (commensurate) with the matrix, with the atomic planes on the two sides of the interface being in perfect register with each other. The mismatch is accommodated by an elastic strain in the epilayer giving a biaxial stress of [3]

2μ f · (1 + ν)

(1 – ν)

(1)

where μ is the shear modulus, ν Poisson's ratio and f the misfit parameter. Elastic isotropy is assumed. The misfit parameter is given by f = (a_e -a_m)/a_m, where a_e , a_m are the lattice parameters of the unconstrained epilayer and matrix in the plane parallel to the interface.

How did he get this formula? Well, this is easy, but deriving the starting formula also illustrates a certain problem one might encounter from looking at simple pictures all the time. Let's see:

If you strain the lattice of the epitaxial layer in one dimension, so that it fits the matrix perfectly, you have the following situation:

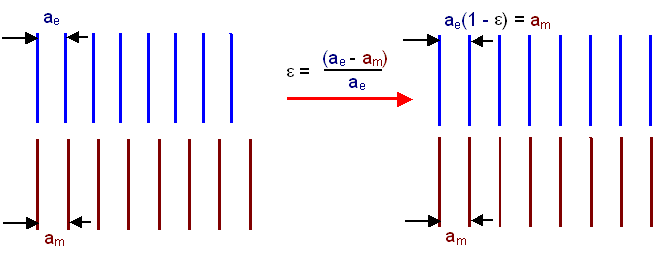
The strain ε needed for perfect fit is ε = (a_e – a_m)/a_e; but since a_e and a_m are nearly equal, dividing by a_e (as is correct) or by a_m (as Sir Peter does) makes no difference. So we can equate ε with f = (a_e – a_m)/a_m, the misfit parameter according to Sir Peter.

Strain ε and stress σ are usually related by
σ = E · ε with E = modulus of elasticity (Youngs modulus).
But since E can be expressed in terms of the shear modulus μ and Poissons ratio ν by
E = 2μ(1 + ν), we can write
σ = 2μ(1 + ν) · ε = 2μ(1 + ν) · f

Apart from the factor (1 – ν), this is Sir Peters starting formula. Where does the (1 – ν) come from?

Let's look at the problem carefully. We actually have a two-dimensional problem and must consider biaxial stress. Our simple figure was one-dimensional - and that is where we might have missed something.

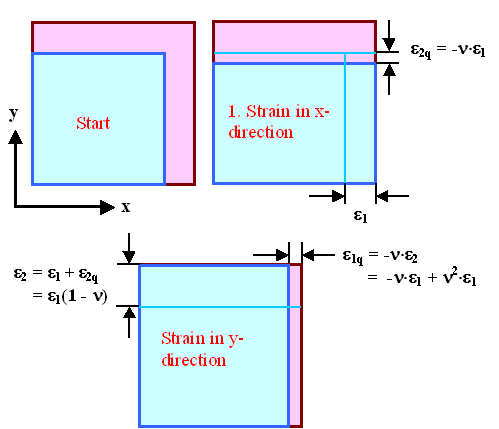
Did we miss something? Well, yes - we did. In the picture above, we have applied a suitable stress to strain the blue lattice to the desired value in the x-direction. If we now apply the same stress in the y-direction perpendicular to the first one, we will have to use a larger strain because the y-dimension of the crystal layer will now be smaller as expressed by Poissons modulus. This is illustrated below.

After we pulled the blue crystal sheet to the desired dimension by a strain ε₁, its lateral dimension in y direction decreased by ε_2q as shown. We now must apply a strain of ε₂ = ε₁(1 – ν) to make the match in y-direction.

That's it. For reasons of symmetry, this must be the strain corrected for biaxial stress in both directions, i.e. we have
ε₁ = ε_1,2/(1 – n)
This is the expression used by Sir Peter.

Of course, we made a little mistake. The deformation in y-direction will lead to a shrinkage in x -direction which me must compensate, which in turn will lead to a shrinkage in y-direction, which will lead to a shrinkage - and so on ad infinitum.

But all this does is to add higher order terms in ν which we commonly neglect in linear elasticity theory.

For the case of Ge_xSi_1-x alloys Vegard's law is approximately obeyed [4], i.e. a_GeSi = a_Si+(a_Ge - a_Si)x, where the a's are the lattice parameters. This means that for Ge_xSi_1-x epilayers on an Si(001) surface, f is a linear function of x; since the lattice parameter of Ge (0.5657nm) is greater than that of Si (0.5431nm), f increases with x (f(x) =0.042x), and the epilayer is in compression. Beyond a critical strain and/or thickness it becomes energetically favourable for the misfit to be accommodated by a network of interface dislocations. In view of the importance of strained epilayers or superlattices for device applications [5] and the development of methods of growing them, much research. has been devoted in recent years to the conditions which control the relaxation of elastic strain by the introduction of misfit dislocations, and to the mechanisms by which they are formed. This paper presents a brief review of this field of research; it does not pretend to be exhaustive.

2. Energetic Considerations

The energy of the system involving a strained epilayer and an array of misfit dislocations is generally discussed for the case of the layer and matrix material being cubic, and the interface parallel to a cube plane. The energy per unit area of a square grid of edge dislocations, Burgers vector b, with dislocation spacing p is given approximately by

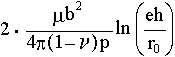(2')

where h is the film thickness, r₀ the core radius, and where the factor 2 arises because of the presence of two orthogonal sets of edge dislocations.

	First, there is a slight correction in eq: (2): The "x" after the "2" as shown in the original has been replaced by a dot - because the "×", writtenas "x" as a sign for multiplication is no longer allowed; it has been used up as denoting the amount of Ge in the alloy Ge_xSi_{1 – x}.
	Now the formula contains an unexplained "e". Since we know that the energy of a dislocation contains the term ln(R/r₀) with R being some outer radius, it is clear that R cannot be larger than h, the thickness of the layer. But by simply equating R with h, we make some numerical mistake which we might correct by introducing a unspecified (but probably not very large) correction factor e?
		That was my first thought. Well - wrong! Sir Peter simply takes one of the many formulas for the total energy of a dislocation that float around, it is the same formula as shown before (for the purpose of recalling it here), and e is e indeed - the base for natural logarithms.
	We then have the correct formula except for the 2/p. But this is easy and pointed out (albeit somewhat obliquely) by Sir Peter:
		The general formula for the dislocation energy gives the energy per unit length of the dislocation. If we want the energy per unit area, we have to multiply by the length of the dislocations in an unit areas and then divide by the unit area.
		If we take the unit area to be p², the areas of one cell of the (square) dislocation network, it contains dislocations with the length 2p - we have the factor 2/p.

The elastic strain remaining is given by ε = f – b/p.

	This is something easy to figure out for yourself. Just take into account that every dislocation with a Burgers vector b relaxes the total deformation by one b (provided it is fully contained in the plane of the boundary).
		Full relaxation thus would occur if a misfit dislocation network with a spacing p = b/f = b/(a_e – a_m)/a_m is introduced which partially relaxes the epitaxial layer.
		The essential trick is to generate a variable ε which is the residual strain contained in a partially relaxed epitaxial layer. So some of the strain and its energy is gone, but at a cost: Dislocations, carrying their own energy penalty, are introduced.
		Since ε is a variable, it can now be used to optimize the system as we will see.

The total energy per unit area E is then given by

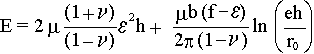(3)

where the first term is the elastic strain energy.

	Here Sir Peters gets a bit tricky once more. The elastic energy E_elast of an uniaxially elastically deformed material is simple σ·ε/2. For biaxial strain its twice that, and that gives the first term.
	The second term is the energy of the dislocation network, it is almost the formula from above.
		However, p has been replaced using the relation ε = f – b/p, or p = b/ (f – ε).
	The next part is straight forward. The total energy per unit area is a function of ε, the strain still present in the epitaxial layer even after some dislocations have been introduced.
		So we can find the minimum energy of the system with respect to ε by calculating dE/dε = 0.
		The calculation is straight forward:

For a given thickness the minimum energy occurs for a value ε₀ given by

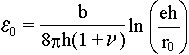(4)

If ε₀ = f, then the layer is ideally commensurate with the substrate, and the elastic strain is equal to f. If ε₀< f then some misfit will be relaxed by dislocations, the spacing being given by (5) with ε₀= f – b/p. The critical film thickness, h_c, at which it becomes energetically favourable for the first dislocation to be introduced is obtained with ε₀ = f, i.e.

	Got it? Well, lets look at the argumentation in detail?
		If the remaining strain ε₀= f, then it is the strain of the unrelaxed layer and the formula defining ε yields b/p = 0 which, since b has a defined value, can only mean p is infinite - in other words there is no dislocation network.
		If ε₀ > f, the layer is not ideally commensurate with the substrate as stated in the original, but a dislocation network must be present (b/p < 0 is required) which increases the strain - the sign of b is the wrong way around. This is of course a totally unphysical high energy situation, and we can safely exclude ε₀ > f from the possible range of ε values.
		If ε₀ < f, again a dislocation network must be present, but this time with the right sign of b - it decreases the total elastic strain.
	Now, ε₀, the optimal residual strain is a function of the layer thickness h. It decreases with increasing h and this means that dislocations must be introduced at some critical thickness h_c.
		If the thickness is below h_c, we have no dislocations and ε = f obtains.
		If the thickness is above h_c, we have dislocations and ε < f obtains.
	This leaves us with ε₀= f at the point of critical thickness. All we have to do now is to express the equation above for h; it will then give h_c by substituting f for ε₀.
		Sir Peter now writes

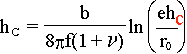(5)

	Two points should be made about this relation:
		First, the above version of equation (5) corrects the little mistake of the original of forgetting the index "c" at the h in the argument of the logarithm, and
		Second; this equation is now a transcendent equation for h_c; we cannot write it down in closed form.

Two points should be made about this relation. First, h_c depends on the core radius r₀ (» b), and the uncertain value of this parameter introduces some uncertainty into this relation, particularly for small h/r₀. Secondly, h_c depends on the assumed dislocation arrangement; for example the misfit might be relieved by dislocations with different b; eqn. (2) shows that the dislocation strain field energy is smaller for edge dislocations of smaller energy, even though for the same relief of strain (f – ε), the spacing p will be smaller. Thus it is necessary to take care in making comparisons between theory and experiment. In practice, however, it is generally found that the observed values of h_c are larger than those predicted over most of the range of misfits (see for example People and Bean [6] for Ge-Si layers on (100) Si). The reasons for this discrepancy are partly due to insensitivity of the experimental techniques used, and partly kinetic in origin. In order to introduce dislocations, there have to be mechanisms for doing so, and for most practical cases, except these with very large misfits, the strain relief is limited by kinetic considerations.

Now, what order of magnitude do we get for h_c, forgetting about the small detail of unclear core radii and so on?

Well, if we rewrite the above equation, with 8π(1 + ν) » 30, and ln eh_c/r₀ = y, we have
h_c » b/f · (ln y)/30

How large is ln y? If we take r₀ to be about 0,3 nm, and eh_c to be anywhere between 10 nm and 1000 nm, we have a range of values from ln(10/0,3) = 3, 51 to ln(1000/0,3) = 8,11).

In other words, it doesn't matter much for orders of magnitude. Lets take an intermediate value of 5 and we get
h_c » b/6 · f.

Now here is a simple formula!

But how good is it? Well, we live in the age of easy accessible PCs with tremendous computing power, so solving the transcendental equation from above is actually no problem at all. The result for a suitable set of parameters is shown in the backbone part of the Hyperscript; here we only note:

The best approximation is actually obtained for ln y = 3,03 leading to

h_c »	b 9.9 · f

So if your misfit is 1% (f = 0,01), your critical thickness will be roughly around 10 b. Burger vectors usually are b = a/2<110> or b = a/2^1/2 which is around 0,3 nm. This gives
h_c » 3 nm - which is not all that much!

Fortunately, as Sir Peter points out in the remainder of the article, the critical thicknesses observed are usually considerably larger than the calculated ones.