Titanium alloys are useful in corrosive or high temperature environments, and possess an attractive strength-to-weight ratio. Replacing heavier steels with Ti alloys in transportation—especially naval—can increase energy efficiency in the transportation of goods. It can be found in hexagonal-closed packed, body-centered cubic, and hexagonal omega phases, and present interesting fundamental material science questions and interesting science and engineering challenges.

Boundaries—grain, twin, or interphase—can act as barriers and sources for dislocations in metals. Understanding their effect on mechanical behavior at the atomistic scale is important for any metal system, and Ti makes for a useful model system to consider in particular the effect of twin boundaries on the motion of line defects like dislocations and disconnections. We use DFT with LGF-based flexible boundary condition methods to study line defects interacting with boundaries in Ti.

Oxygen is a ubiquitous interstitial element in Ti; it adds solution strengthening at low concentrations but leads to ductility losses at higher concentrations. Higher concentrations are avoided by maintaining alloys below 550°C, which limits oxygen mobility from the native oxide (alpha case) into the Ti matrix. We use DFT techniques to determine the diffusion mechanism for oxygen in alpha-Ti.

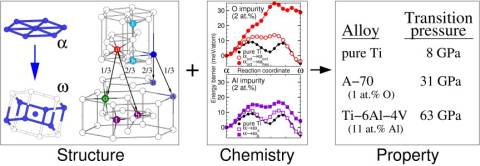
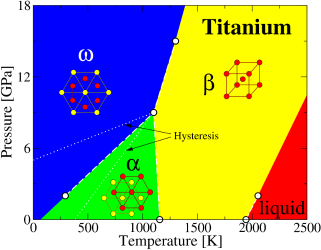
Martensitic phase transformations are structural phase transitions that occur without diffusion; they can propagate near the speed of sound. The formation of martensitic phases are key to geophysical processes, strengthening in steels, and the shape-memory effect. In Ti, the high pressure omega phase embrittles alpha (hcp) Ti alloys. However, as little as 1at.% oxygen can push the transformation pressure from 9GPa up to more than 35GPa. Modeling changes in the transformation with solutes and interstitials requires (1) the atomistic mechanism, and (2) calculation of changes in the energy barrier. A new algorithm was developed that permits systematic generation and sorting (by energy barrier) of transformation pathways; this algorithm found a new low energy barrier pathway for Ti alpha-omega called TAO-1. The change in energy barrier from different solutes predicts changes in transition pressure for engineering Ti alloys.

1. “Classical potential describes martensitic phase transformations between the alpha, beta and omega titanium phases”
   R. G. Hennig, T. J. Lenosky, D. R. Trinkle, S. P. Rudin, and J. W. Wilkins. Phys. Rev. B 78, 054121 (2008): publication, PDF, doi, preprint
2. “Lattice and elastic constants of titanium-niobium monoborides containing aluminum and vanadium”
   D. R. Trinkle. Scripta Mater. 56, 273-276 (2007): publication, PDF, doi, preprint
3. “An Empirical Tight-Binding Model for Titanium Phase Transformations”
   D. R. Trinkle, M. D. Jones, R. G. Hennig, S. P. Rudin, R. C. Albers, and J. W. Wilkins. Phys. Rev. B 73, 094123 (2006): publication, PDF, doi, preprint
4. “Systematic pathway generation and sorting in martensitic transformations: Titanium alpha to omega”
   D. R. Trinkle, D. M. Hatch, H. T. Stokes, R. G. Hennig, and R. C. Albers. Phys. Rev. B 72 014105 (2005): publication, PDF, doi, preprint
5. “Impurities block the alpha to omega martensitic transformation in Titanium”
   R. G. Hennig, D. R. Trinkle, J. Bouchet, S. G. Srinivasan, R. C. Albers, and J. W. Wilkins. Nature Materials 4(2), 129-133 (2005): publication, PDF, doi, preprint
6. “A New Mechanism for the Alpha to Omega Martensitic Transformation in Pure Titanium”
   D. R. Trinkle, R. G. Hennig, S. G. Srinivasan, D. M. Hatch, M. D. Jones, H. T. Stokes, R. C. Albers, and J. W. Wilkins. Phys. Rev. Lett. 91, 025701 (2003): publication, PDF, doi, preprint
7. “Shock-Induced alpha-omega Transition in Titanium”
   C. W. Greeff, D. R. Trinkle, and R. C. Albers. J. Appl. Phys. 90 5, p. 2221-6 (2001): publication, PDF, doi

The work on diffusion is in collaboration with Don Shih at Boeing, and is funded by a grant from Boeing. The work on interfaces in Ti is funded through the NSF CAREER program. Previous work on phase transformations was in collaboration with John Wilkins at Ohio State, Richard Hennig at Cornell, Bob Albers and Sven Rudin at LANL, Srivilliputhur Srinivasan at North Texas University, and Dorian Hatch and Harold Stokes at Brigham Young University. Computational resources are provided through the NSF TeraGrid program.